 La méthode de calcul du TEG ou Taux Effectif Global d’un emprunt est définie par les textes et annexes du Code de la Consommation.
La méthode de calcul du TEG ou Taux Effectif Global d’un emprunt est définie par les textes et annexes du Code de la Consommation.
Le TEG pour les crédits à la consommation
Le TEG est un taux annuel, à terme échu, calculé selon la méthode d’équivalence. On parlera aussi (mais pas obligatoirement) de TAEG ou de Taux Actuariel Effectif Global pour le TEG des prêts à la consommation.
Le TEG pour les crédits immobiliers et les crédits professionnels
Pour ces deux catégories de crédits, le TEG doit être calculé en deux étapes. La première étape consiste à calculer un taux périodique correspondant à la périodicité des remboursements (sans que cette période soit inférieure à un mois) par la méthode d’équivalence. Le TEG annuel s’obtient ensuite de manière proportionnelle en multipliant le taux périodique par le nombre de périodes dans l’année. On parlera de TEG proportionnel pour cette méthode.
La réglementation du mode de calcul du TEG
Le mode de calcul du TEG est défini par l’article de loi suivant : « Sauf pour les opérations de crédit mentionnées au 3° de l’article L. 311-3 et à l’article L. 312-2 du présent code pour lesquelles le taux effectif global est un taux annuel, proportionnel au taux de période, à terme échu et exprimé pour cent unités monétaires, le taux effectif global d’un prêt est un taux annuel, à terme échu, exprimé pour cent unités monétaires et calculé selon la méthode d’équivalence définie par la formule figurant en annexe au présent code. Le taux de période et la durée de la période doivent être expressément communiqués à l’emprunteur. Le taux de période est calculé actuariellement, à partir d’une période unitaire correspondant à la périodicité des versements effectués par l’emprunteur. Il assure, selon la méthode des intérêts composés, l’égalité entre, d’une part, les sommes prêtées et, d’autre part, tous les versements dus par l’emprunteur au titre de ce prêt, en capital, intérêts et frais divers, ces éléments étant, le cas échéant, estimés. Lorsque la périodicité des versements est irrégulière, la période unitaire est celle qui correspond au plus petit intervalle séparant deux versements. Le plus petit intervalle de calcul ne peut cependant être inférieur à un mois. Pour les opérations mentionnées au 3° de l’article L. 311-3 et à l’article L. 312-2, lorsque les versements sont effectués avec une fréquence autre que annuelle, le taux effectif global est obtenu en multipliant le taux de période par le rapport entre la durée de l’année civile et celle de la période unitaire. Le rapport est calculé, le cas échéant, avec une précision d’au moins une décimale.»
Le texte tel qu’il est rédigé est applicable depuis le 1er juillet 2002. Les parties du texte qui sont en caractère gras ont été ajoutées lors de la dernière modification, par le décret 2002-927 du 10 juin 2002 relatif au calcul du taux effectif global. Ce décret est la transposition en droit français de la directive du Parlement européen et du Conseil du 16 février 1998. Il faut comprendre le texte de la façon suivante : Les opérations mentionnées au 3° de l’article L311-3 : ce sont les opérations « destinés à financer les besoins d’une activité professionnelle, ainsi que les prêts aux personnes morales de droit public. » Les opérations mentionnées à l’article L313-2 : ce sont les opérations « consentis de manière habituelle par toute personne physique ou morale en vue de financer » l’acquisition, la souscription, les dépenses de construction, de réparation, d’amélioration, d’entretien d’« immeubles à usage d’habitation ou à usage professionnel d’habitation » ou « l’achat de terrains destinés à la construction des immeubles ». Par simplification dans cette page, on parlera pour ces deux catégories, des crédits professionnels et des crédits immobiliers. Pour les autres crédits, on parlera des crédits à la consommation.
Equation de base traduisant l’équivalence des prêts
La formule évoquée dans l’article R313-1 est présente en annexe du Code de la Consommation. Cette annexe a été introduite par le même décret 2002-927 évoqué plus haut. Le décret 2002-928 du 10 juin 2002 complète la formule en y ajoutant des exemples numériques. Cette formule est aussi désignée comme l’équation des intérêts composés ou la formule des flux actualisés (ou formule d’actualisation des flux). Elle se présente de la façon suivante :
Formule des flux actualisés
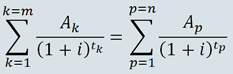
- i : le taux effectif global annuel
- k : le numéro d’ordre d’un déblocage de fond,
- m : le numéro d’ordre du dernier déblocage,
- Ak : le montant du déblocage numéro k,
- tk : l’intervalle de temps entre le premier déblocage et le déblocage numéro k,
- p : le numéro d’ordre d’une échéance de remboursement,
- n : le numéro d’ordre de la dernière échéance,
- Ap : le montant de l’échéance numéro p,
- tp : l’intervalle de temps entre le premier déblocage et l’échéance numéro p.
Dans sa forme générale, les intervalles de temps doivent être exprimés en années et fractions d’années. La plupart du temps, cette équation doit être résolue par approximations successives. Le taux i, résolvant l’équation, peut être arrondi à la première décimale (ce n’est pas une obligation). Les différents montants Ak ou Ap ne sont pas nécessairement égaux entre eux.
Comprendre cette équation
Cette équation représente l’égalité entre la, ou, les mises à disposition des fonds et tous les remboursements ou dépenses, actualisés à la date du premier déblocage. Par exemple, pour une somme de 1.000 euros mise à disposition le 1er janvier et remboursée 90 euros tous frais compris le 1er de chaque mois en 12 mensualités, l’équation peut s’écrire : ![]() Le coefficient de temps de la première mensualité, au 1er février, sera de 31 jours divisé par 365, puis de 59/365 pour celle du 1er mars. Et ainsi de suite, jusqu’à la dernière avec 365/365. Par la résolution de l’équation, on obtient un TEG i = 15,52 %.
Le coefficient de temps de la première mensualité, au 1er février, sera de 31 jours divisé par 365, puis de 59/365 pour celle du 1er mars. Et ainsi de suite, jusqu’à la dernière avec 365/365. Par la résolution de l’équation, on obtient un TEG i = 15,52 %.
Les types de durées à utiliser
L’annexe au Code de la Consommation indique que les durées doivent être exprimé en années et fraction d’années, en précisant, qu’une année compte 365 jours (ou 366 pour les bissextiles) ou 12 mois normalisés. Le mois normalisé comptant 30.41666 jours (soit 365 jours / 12). La durée moyenne de l’année à 365,25 jours, bien que citée dans la directive européenne, n’est pas reprise dans le texte français. Dans les exemples du Code de la Consommation, il apparait qu’à partir du moment où les dates d’échéance sont fixées au même jour de chaque mois, on puisse utiliser la notion de mois normalisé, ou plus simplement une fraction de durée en nombre de mois divisé par 12 mois. L’équation de notre exemple s’écrirait alors : ![]() Le TEG obtenu par la résolution de cette équation est de 15,45 %. A noter qu’ici, il y a une différence de résultat suivant que le calcul est réalisé en nombre de jours réels ou en nombre de jours (ou mois) normalisés. Cependant, cette différence aura un impact limité sur des durées de remboursement de plusieurs dizaines d’années. Par exemple, un crédit de 100.000 € remboursé en 240 mensualités de 600 € aura un TAEG de 3,956 % calculé en nombre de mois et de 3,955 % calculé en nombre de jours réels. Cette méthode présente, en outre, l’avantage de calculer le TEG sur la même base d’une période mensuelle que sont calculées les échéances.
Le TEG obtenu par la résolution de cette équation est de 15,45 %. A noter qu’ici, il y a une différence de résultat suivant que le calcul est réalisé en nombre de jours réels ou en nombre de jours (ou mois) normalisés. Cependant, cette différence aura un impact limité sur des durées de remboursement de plusieurs dizaines d’années. Par exemple, un crédit de 100.000 € remboursé en 240 mensualités de 600 € aura un TAEG de 3,956 % calculé en nombre de mois et de 3,955 % calculé en nombre de jours réels. Cette méthode présente, en outre, l’avantage de calculer le TEG sur la même base d’une période mensuelle que sont calculées les échéances.
Le décalage de l’équation dans le temps
L’équation de base est exprimée en valorisant les flux à la date de déblocage des fonds. En multipliant ou en divisant par un même coefficient d’actualisation, les sommes peuvent être exprimées à une autre date. Pour illustrer cela, notre équation, exprimée à la date de première mensualité, deviendrait : ![]() Cette propriété est utilisée dans plusieurs exemples du Code de la Consommation : un déblocage des fonds le 15 septembre et 36 mensualités chaque dernier jour du mois à compter du 31 octobre. Chaque remboursement est divisé par un coefficient d’actualisation (1+i) avec un exposant variant de 1/12 à 36/12. L’ensemble de la somme des remboursements actualisés étant lui-même divisé par un coefficient d’actualisation de 15 jours (soit 15/365 ou 15.58333/365 suivant la méthode employée).
Cette propriété est utilisée dans plusieurs exemples du Code de la Consommation : un déblocage des fonds le 15 septembre et 36 mensualités chaque dernier jour du mois à compter du 31 octobre. Chaque remboursement est divisé par un coefficient d’actualisation (1+i) avec un exposant variant de 1/12 à 36/12. L’ensemble de la somme des remboursements actualisés étant lui-même divisé par un coefficient d’actualisation de 15 jours (soit 15/365 ou 15.58333/365 suivant la méthode employée). 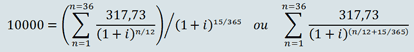
Exemple du TEG d’un crédit immobilier
Comme nous l’avons vu plus haut, le TEG pour un crédit immobilier passe d’abord par le calcul de son taux périodique. Dans la situation classique d’un emprunt débloqué en une seule fois, comportant des remboursements mensuels de 180 échéances. L’équation à résoudre peut être écrite de la façon suivante : ![]() Le déblocage d’un montant capital est effectué en une seule fois. La première mensualité de montant Remb1 est payée un mois après (coefficient 1 mois). La deuxième d’un montant Remb2 est payée le mois suivant. Jusqu’à la 180° de montant Remb180 payée 180 mois après le début. Le montant de chaque mensualité peut être différent. En compliquant un petit peu : déblocage en deux fois à 6 mois d’intervalle et prise en compte de frais de dossier, l’équation deviendra :
Le déblocage d’un montant capital est effectué en une seule fois. La première mensualité de montant Remb1 est payée un mois après (coefficient 1 mois). La deuxième d’un montant Remb2 est payée le mois suivant. Jusqu’à la 180° de montant Remb180 payée 180 mois après le début. Le montant de chaque mensualité peut être différent. En compliquant un petit peu : déblocage en deux fois à 6 mois d’intervalle et prise en compte de frais de dossier, l’équation deviendra : ![]() A noter : Capital1 a comme diviseur un coefficient d’actualisation élevé à la puissance zéro. On aurait pu écrire Capital1 simplement comme dans la formule précédente. Une fois le taux périodique i déterminé, le TEG de ce crédit sera égal à 12 × i.
A noter : Capital1 a comme diviseur un coefficient d’actualisation élevé à la puissance zéro. On aurait pu écrire Capital1 simplement comme dans la formule précédente. Une fois le taux périodique i déterminé, le TEG de ce crédit sera égal à 12 × i.
